What is Intrinsic Carrier Concentration

Intrinsic Silicon Wafers

We have a large selection of intrinsic silicon wafers in stock with resistiivty greater than 20,000 ohm-cm. Please send us your specs for an immediate quote.

Silicon Wafers Quote FAST! Or, Buy Online and Start Research Today!

Enter the code from the image:
Refresh CAPTCHA

What is the intrinsic carrier concentration of silicon?

The intrinsic carrier concentration of silicon at room temperature (around 300 K) is approximately 1.1×1010 1.1 × 10 10 carriers per cubic centimeter (cm−3 −3). This value represents the number of free electrons and holes in pure silicon at this temperature. It's important to note that the intrinsic carrier concentration can vary with temperature, increasing as the temperature rises.

What is the Intrinsic Carrier Concentration of Germanium?

The intrinsic carrier concentration of germanium at room temperature, which is typically considered to be around 300 Kelvin, is approximately 2.5×1013 2.5 × 10 13 carriers per cubic centimeter (cm−3 −3). This value is significantly higher than that of silicon, reflecting the smaller bandgap energy of germanium. Like silicon, the intrinsic carrier concentration in germanium also varies with temperature, generally increasing as the temperature rises.

 

Intrinsic Carrier Concentration

Intrinsic carrier concentration refers to the density of charge carriers—electrons and holes—in a pure (undoped) semiconductor material at thermal equilibrium. In semiconductors such as silicon and germanium, these vital charge carriers enable the material to transmit electrical current.

In an intrinsic (pure) semiconductor, the number of electrons (negative charge carriers) is equal to the number of holes (positive charge carriers). These carriers are generated due to thermal energy which breaks some covalent bonds in the semiconductor lattice, releasing electrons. Each released electron leaves behind a hole. The number of charge carriers in a semiconductor naturally fluctuates, depending on the material's characteristics and how hot it gets, usually rising when things warm up.

Grasping this key idea is vital, as it shapes the way we craft and understand various electronic parts like switches, rectifiers, and energy-harvesting panels. The number of free charge carriers that exist naturally in different types of semiconductors is a critical detail when diving into the world of semiconductor science.

Why is it Important to Know Intrinsic Carrier Concentration

Knowing the intrinsic carrier concentration is important for several reasons in the field of semiconductor physics and electronic engineering:

1. Getting to know the basics of how a semiconductor behaves, like what its band gap energy is, starts with understanding something called intrinsic carrier concentration. The number of free charge carriers in a semiconductor gives us clues about its energy barriers and how easily electrons can jump the gap. It sheds light on how the material will act under various scenarios, particularly when we look at how well it carries an electric current.

2. Lots of gadgets we use, like switches, light-emitters, and sun power catchers, rely on special materials that conduct electricity in a controlled way. A host of gadgets we use every day, from the humble switch to the glowing LED and power-generating solar panels, all rely on materials known as semiconductors. Grasping the natural quantity of charge carriers is vital in tailoring devices like transistors and solar panels, making sure they perform with top efficiency for their designed roles.

3. Temperature Dependence: The intrinsic carrier concentration increases with temperature. Grasping how semiconductor devices act differently as the thermometer climbs or falls is key to making sure they work right and last long.

4. Doping Process: The process of doping adds impurities to a semiconductor to change its electrical properties. To tailor a semiconductor's electric traits to our needs, we've got to grasp the natural number of charge carriers it has so we can figure out just how much extra stuff—dopants—we need to mix in.

5. Material Selection: Different semiconductor materials have different intrinsic carrier concentrations. This parameter is one of the factors considered when selecting a material for a specific electronic application.

6. Analysis of P-N Junctions: Grasping the role of intrinsic carrier density is crucial when dissecting the inner workings of p-n junctions, which are essential elements in a plethora of electronic gadgets. It's key to grasp how these junctions act, since it shapes the way we craft things like diodes and transistors—those tiny parts at the heart of our electronic gadgets.

7. Understanding and Controlling Leakage Currents: In some semiconductor devices, especially in high-temperature environments, leakage currents due to intrinsic carrier generation can affect the performance. Grasping the amount of charge carriers that are naturally present is key to reigning in these pesky currents that might throw a wrench in our semiconductor operations.

In essence, the number of carriers that naturally exist in a semiconductor is a critical factor shaping how it conducts electricity and impacts the way we craft and enhance our electronic materials and gadgets. Grasping this concept is crucial for crafting and enhancing a variety of gadgets that keep us plugged in and powered up.

How do you Calculate Intrinsic Concentration?

The intrinsic carrier concentration (n_i) in a semiconductor can be calculated using a formula that depends on
The intrinsic carrier concentration (n_i) in a semiconductor can be calculated using a formula that depends on factors like the material's properties and temperature. The general expression is:

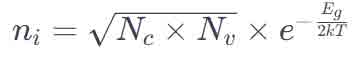
Where:

• Nc​ is the effective density of states in the conduction band.
• Nv​ is the effective density of states in the valence band.
• Eg​ is the energy gap (bandgap) of the semiconductor.
• k is Boltzmann's constant (8.617 x 10^-5 eV/K).
• T is the absolute temperature in Kelvin.

Here's a brief explanation of each component:

1. Effective Density of States (Nc​ and Nv​ ): These values represent the number of available states for electrons in the conduction band and for holes in the valence band, respectively. They depend on the material's properties and temperature. The expressions for Nc​ and Nv​ typically involve material constants and temperature.
2. Bandgap Energy (Eg​ ): This is the energy difference between the top of the valence band and the bottom of the conduction band. It's a characteristic property of the semiconductor material.
3. Exponential Term: The term e - Eg/2kT​ represents the probability of an electron gaining enough thermal energy to jump from the valence band to the conduction band, thus creating an electron-hole pair. It shows how the intrinsic carrier concentration increases with temperature and decreases with a larger bandgap.

This formula provides an approximation for the intrinsic carrier concentration under thermal equilibrium conditions. The actual calculation would require specific values for Nc, Nv​, and Eg​ for the semiconductor material in question, as well as the temperature at which the semiconductor is operating.